PyTorch 线性回归

根据历史数据预测未来的房价。实现一个线性回归模型，用梯度下降算法求解该模型，给出预测直线。

Note

本实例来自《深度学习原理与PyTorch实战（第2版）》，本文是我对该节的自学实践。

四大步骤：准备数据、设计模型、训练和预测

准备数据

采用认为编造数据。创建 100 个时间节点：

x = torch.linspace(0, 100, 100).type(torch.FloatTensor)

创建随机房价数据：

rand =torch.randn(100)* 10
y = x + rand

数据集训练集切分：

x_train = x[: -10]
x_test = x[-10 :]
y_train = y[: -10]
y_test = y[-10 :]

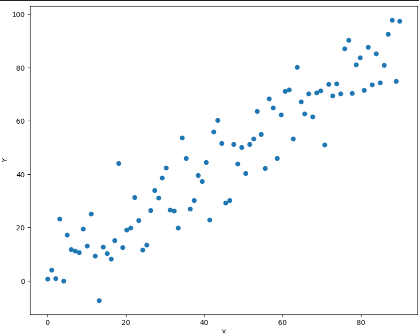
训练数据可视化：

import matplotlib.pyplot as plt # 导入画图的程序包
plt.figure(figsize=(10,8)) # 设定绘制窗口大小为10×8 inch
# 绘制数据，由于x和y都是自动微分变量，因此需要用data获取它们包裹的tensor，并转成NumPy 
plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'o')
plt.xlabel('X') # 添加X轴的标注
plt.ylabel('Y') # 添加Y轴的标注
plt.show() # 画出图形

设计模型

需要拟合的方程是： $y = a x + b$ ，需要通过模型估算的是 a 和 b。

定义一个平均损失函数：

L (a, b) = \frac{1}{N} \sum_{i} (y_{i} - {\hat{y}}_{i})^{2} = \frac{1}{N} \sum_{i} (y_{i} - a x_{i} - b)^{2}

L 是一个关于 a 和 b 的非线性函数。目标是让 L 尽可能的小。

上面训练集的坐标点，都通过累加融入进 L 当中。

这里使用梯度下降法。给一个初始坐标，沿着梯度下降的方式，寻找 L 的最小值。

下山的步子大小叫做学习率。

训练

定义两个自动微分变量：

a = torch.rand(1, requires_grad = True)
b = torch.rand(1, requires_grad = True)

学习率：

learning_rate = 0.0001

用代码实现上面的公式：

for i in range(1000):
  # 计算在当前a、b条件下的模型预测值
  predictions = a.expand_as(x_train) * x_train + b.expand_as(x_train)
  # 将所有训练数据代入模型ax+b，计算每个的预测值。这里的x_train和predictions都是(90, 1)的张量
  # Expand_as的作用是将a、b扩充维度到和x_train一致
  loss = torch.mean((predictions - y_train) ** 2) # 通过与标签数据y比较计算误差，loss是一个标量
  print('loss:', loss)
  loss.backward() # 对损失函数进行梯度反传
  # 利用上一步计算中得到的a的梯度信息更新a中的data数值
  a.data.add_(- learning_rate * a.grad.data)
  # 利用上一步计算中得到的b的梯度信息更新b中的data数值
  b.data.add_(- learning_rate * b.grad.data)
  # 增加这部分代码，清空存储在变量a、b中的梯度信息，以免在backward的过程中反复不停地累加
  a.grad.data.zero_() # 清空a的梯度数值
  b.grad.data.zero_() # 清空b的梯度数值

思维模式

如何建立对这种代码的思维模式？

让我们把这个深度学习的训练过程比作是尝试调整一架非常复杂的遥控飞机，让它飞得更稳、更远。这里，a和b可以看作是控制飞机的两个旋钮，x_train是飞机每次尝试飞行时的不同起飞角度，y_train是我们希望飞机达到的目标高度。

初始化：一开始，我们随机调整这两个旋钮a和b，我们不知道正确的调整方式，所以飞机的飞行表现可能会很差。
预测阶段：对于每一个起飞角度（x_train），我们根据当前的旋钮设置（a和b的值）预测飞机能飞多高。这个预测就是通过公式a * x_train + b来计算的，就像根据飞机的起飞角度和旋钮的设置来估计它的飞行高度。
计算误差（损失）：然后，我们看看飞机实际飞得有多高（predictions）与我们希望它飞得高度（y_train）之间有多大差距。我们用所有飞行尝试的平均误差来衡量这个差距，这就是loss。如果loss很大，说明我们的旋钮设置得不好，飞机飞得不够理想。
调整旋钮（更新a和b）：为了让飞机飞得更好，我们需要根据误差来调整旋钮a和b。这个调整过程是通过一种叫做梯度下降的方法来完成的。简单来说，就是看看调整旋钮使误差增大还是减小，然后往让误差减小的方向调整。loss.backward()这一步就是为了计算出旋钮调整的方向和幅度，然后我们根据这个信息来实际调整旋钮，即更新a和b的值。
重复尝试：我们重复这个过程很多次（这里是1000次）。每次都根据上一次的飞行结果来调整旋钮，试图让飞机飞得更高。
清零梯度：每次调整旋钮之后，我们需要清除上一次的调整记录（梯度），就像把上一次飞行的数据从黑匣子中删除，以便新的飞行尝试不会受到上一次尝试的影响。

这个过程就像是一个不断尝试和调整的过程，目的是找到最好的旋钮a和b的设置，使得飞机能在各种不同起飞角度下都能飞得尽可能接近我们希望的高度。在深度学习中，我们通过这种方式来“训练”模型，让它在处理数据时表现得更好。

那为什么每次 backward 都会越调越好呢，而不是约调越差？我想，因为 L 是一个关于 a 和 b 的非线性函数，我们可以对其求偏微分，这个偏微分其实是数据无关的，即与第一次算出来的 L 也没有关系。偏微分和学习率是相关的，第一次 backward，我们在超曲面上，移动到一个新的点，即新的 a,b，由于是沿着微分（梯度）下降方向，所以下一次的 L 一定更小，除非说我们的学习率过大，导致错过了最优点，会出现先下降再上升的情况。我理解的对吗？

你的理解基本正确，让我帮你梳理一下这个过程。

在深度学习中，我们的目标是最小化损失函数（L），它衡量了模型预测值和真实值之间的差距。损失函数是关于模型参数（本例中是a和b）的函数。通过调整这些参数，我们希望找到一组使得损失函数值最小的参数，这意味着模型的预测值非常接近真实值。

为什么会越调越好？

梯度方向：当我们对损失函数L关于参数a和b进行偏微分，我们实际上得到的是损失函数在当前参数值下的梯度。这个梯度指向的是损失函数增长最快的方向。因此，如果我们希望减少损失（即让L变小），我们需要沿着梯度的反方向更新参数，这样就能朝着损失函数减小的方向前进。
学习率的作用：学习率决定了我们每次更新参数时应该走多远。如果学习率设置得太小，更新的步伐会非常缓慢，需要很多次迭代才能接近最优点；如果学习率太大，可能会在最优点附近“跳跃”，导致损失函数值反而增加。合适的学习率可以帮助我们有效地接近最优解。
调整方向：在每次迭代过程中，我们根据损失函数的梯度来调整参数a和b。由于我们是沿着梯度的反方向调整参数的，这就意味着我们正在尝试减少损失函数的值。因此，如果学习率选择得当，每次迭代后的L理应是减小的，表明我们的模型在逐渐改进。

注意

局部最小值和全局最小值：在某些复杂的损失函数中，可能存在多个局部最小值点。梯度下降方法可能会导致我们找到的是一个局部最小值而不是全局最小值。这取决于参数的初始值和损失函数的形状。
学习率和调整策略：对于学习率而言，存在一些高级的调整策略，如动态调整学习率、使用动量等，这些策略可以帮助我们更有效地找到最优解，避免上述的一些问题。

总之，通过沿着梯度的反方向调整参数，我们能够使得损失函数的值逐渐减小，从而使模型的性能逐步提升。但是，这个过程需要合理选择学习率，并且可能需要一些技巧来避免陷入局部最小值，或者处理其他可能的优化挑战。

在上述例子中，a、b 就是神经网络的参数。一次迭代就是一次训练。

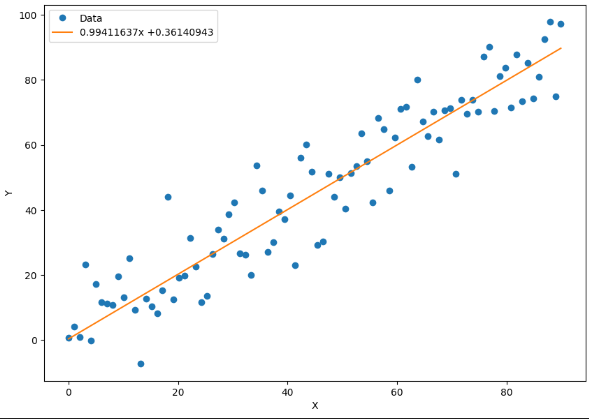
绘制拟合结果

x_data = x_train.data.numpy() # 将x中的数据转换成NumPy数组
plt.figure(figsize = (10, 7)) # 定义绘图窗口
xplot, = plt.plot(x_data, y_train.data.numpy(), 'o') # 绘制x和y的散点图
yplot, = plt.plot(x_data, a.data.numpy() * x_data +b.data.numpy()) # 绘制拟合直线图
plt.xlabel('X') # 给横坐标轴加标注
plt.ylabel('Y') # 给纵坐标轴加标注
str1 = str(a.data.numpy()[0]) + 'x +' + str(b.data.numpy()[0]) # 将拟合直线的参数a、b显示出来
plt.legend([xplot, yplot],['Data', str1]) # 绘制图例
plt.show() # 绘制图形

预测

首先用测试集的 x 算出预测：

predictions = a.expand_as(x_test) * x_test + b.expand_as(x_test) # 计算模型的预测结果
predictions # 输出

在放到图中一起比较：

x_data = x_train.data.numpy() # 获得x包裹的数据
x_pred = x_test.data.numpy() # 获得包裹的测试数据的自变量
plt.figure(figsize = (10, 7)) # 设定绘图窗口大小
plt.plot(x_data, y_train.data.numpy(), 'o') # 绘制训练数据
plt.plot(x_pred, y_test.data.numpy(), 's') # 绘制测试数据
x_data = np.r_[x_data, x_test.data.numpy()]
plt.plot(x_data, a.data.numpy() * x_data + b.data.numpy()) # 绘制拟合数据
plt.plot(x_pred, a.data.numpy() * x_pred + b.data.numpy(), 'o') # 绘制预测数据
plt.xlabel('X') # 更改横坐标轴标注
plt.ylabel('Y') # 更改纵坐标轴标注
str1 = str(a.data.numpy()[0]) + 'x +' + str(b.data.numpy()[0]) # 图例信息
plt.legend([xplot, yplot],['Data', str1]) # 绘制图例
plt.show()

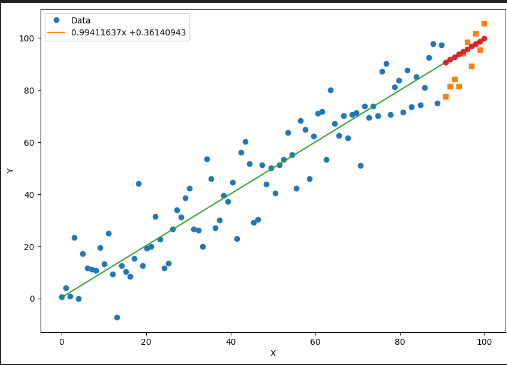
红点是预测值，黄点是实际值。

本文作者：Maeiee

本文链接：PyTorch 线性回归

版权声明：如无特别声明，本文即为原创文章，版权归 Maeiee 所有，未经允许不得转载！

喜欢我文章的朋友请随缘打赏，鼓励我创作更多更好的作品！